Mathematical optimization

In the last 50 years, mathematical optimization models and algorithms have proven their universal applicability in many areas of decision and planning support. Especially in the last two decades, mathematical research has contributed to the development of modern optimization algorithms, which nowadays can be used to handle problem sizes that seemed unthinkable 10 years ago. Thus, linear programs with billions of variables and constraints can be solved efficiently, and for integer programs one is already in the million range. An overview of the past increases in efficiency in solver development is given in the following diagram using the example of two leading commercial solvers for this type of problem.

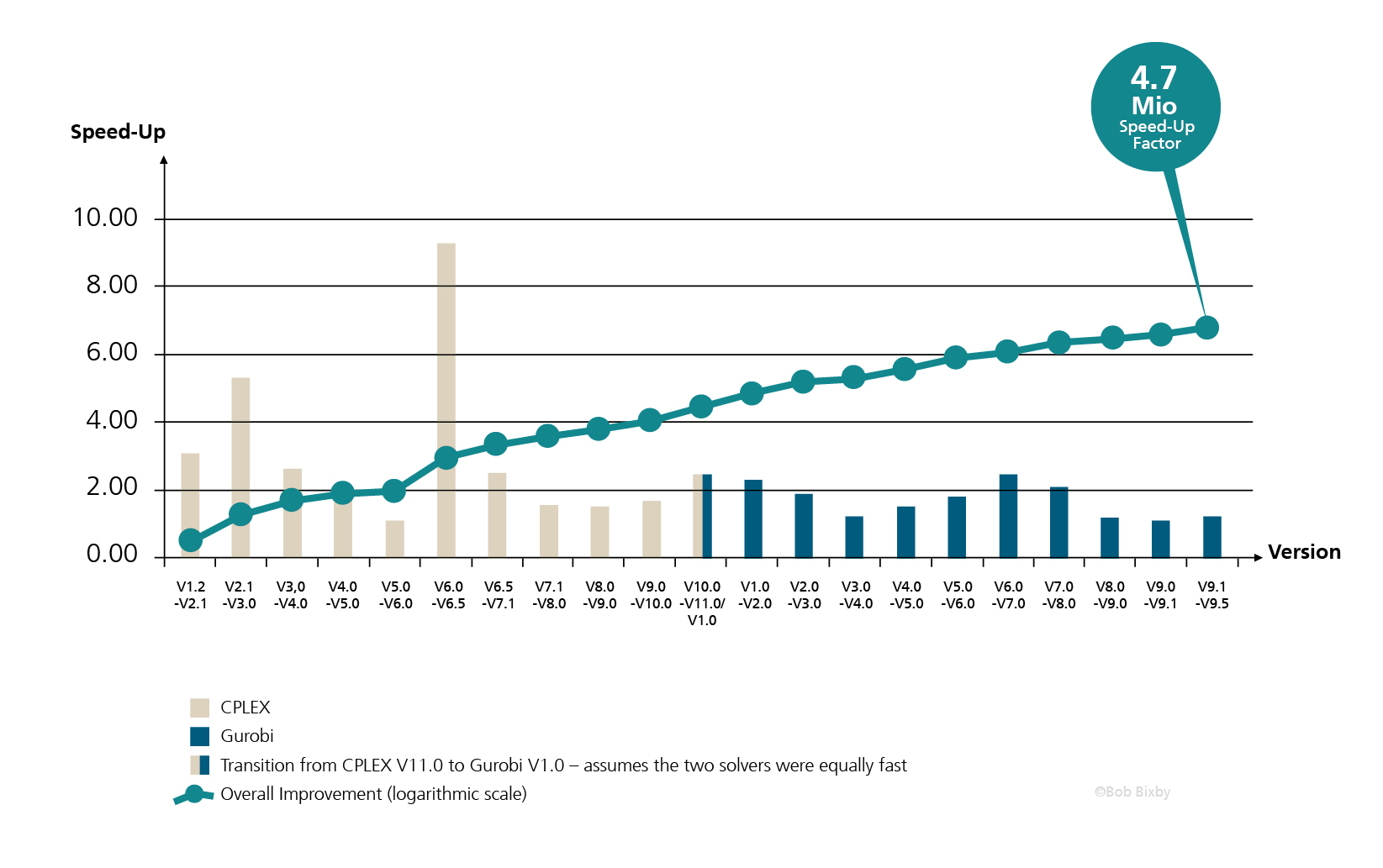
As can be seen, the development of better mathematical methods alone has resulted in a speed-up factor of 4.7 million. In comparison, the speed-up factor due to better hardware is just 1600. All in all, this means that optimization problems can now be solved within 1 second that seemed unsolvable 25 years ago.

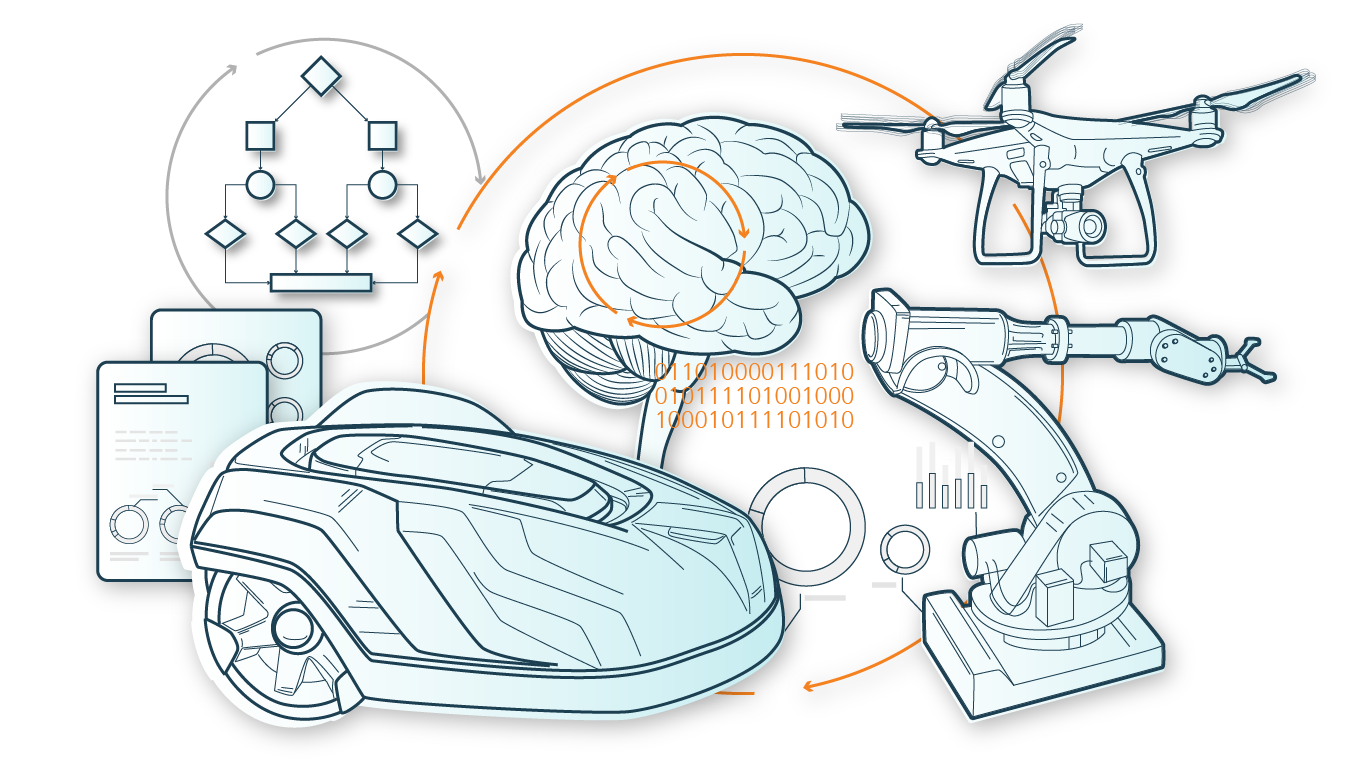
From planning to real-time optimization

The partners in the ADA Lovelace Center have been developing efficient mathematical methods for planning problems of all kinds for many years. This includes, for example, the fields of transportation and logistics, power generation and transmission, supply chain management, building infrastructures, automotive, finance, and engineering applications. At the same time, optimization-theoretic problems are examined and their results are used, for example, in the acceleration of general solver codes.
Recently, the integration of machine learning methods with optimization methods has opened up a whole new field in terms of moving from offline optimization problems (with known, static parameters) to online optimization problems in real-time applications (under dynamic, time-varying parameters). For the often highly dynamic constraints of today's applications, e.g., logistics chain planning, the availability of such methods will be of particular importance. For example, we have shown that it is possible to derive priorities and cost functions in planning problems from observed past decisions. The ability to derive explicit planning rules from past decisions therefore provides greater automation and objectifiability of the planning decisions to be made. The further development of such approaches within the framework of learning methods is of particular importance at the ADA Lovelace Center. Our work makes it possible for the first time to turn the quality guarantees of these methods, which have so far only existed in theory, into practically usable algorithms that provide the user with a decisive competitive advantage.

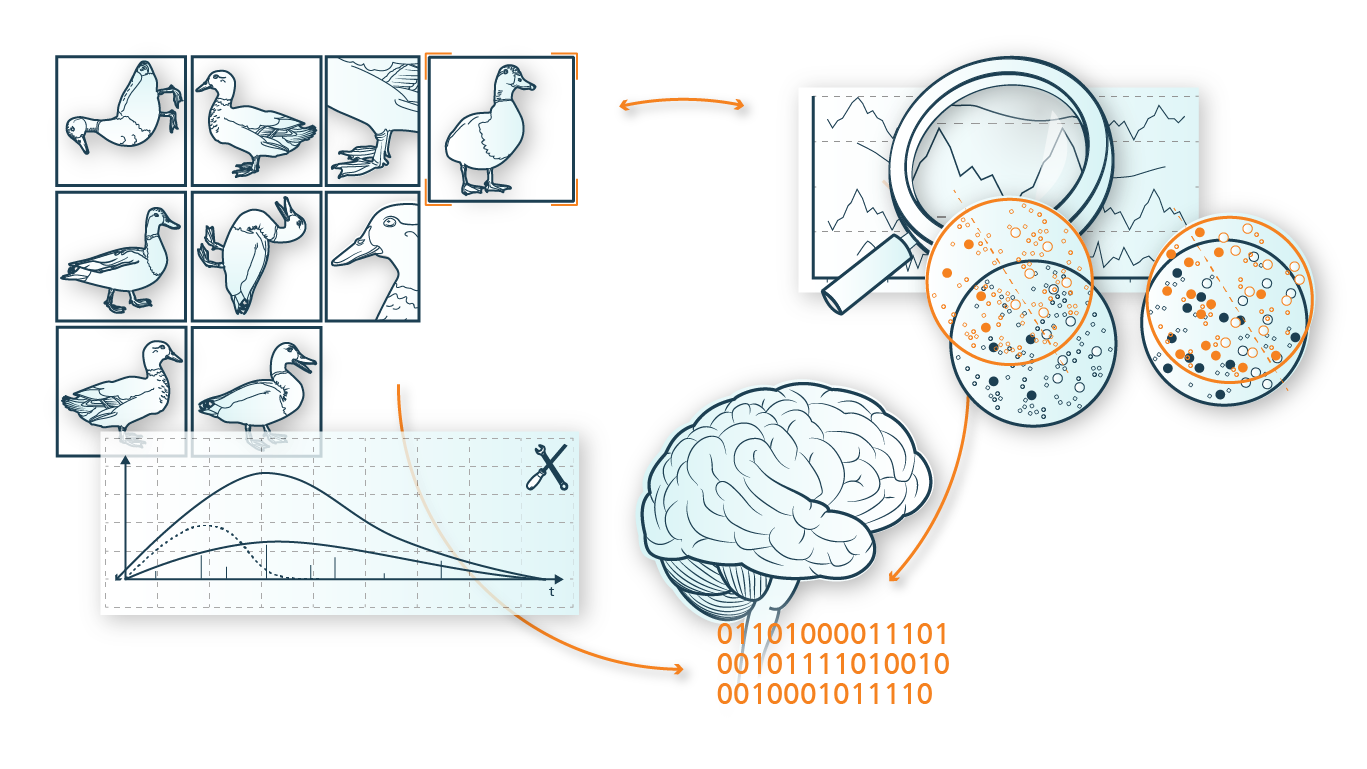
Co-learning mathematical decision models by combining data analysis and optimization

Data analysis and optimization have traditionally been two separate, sequential steps in the development of decision support systems. However, this approach is increasingly reaching its limits for several reasons: In the age of increasingly large data sets, simply selecting the parameters relevant to an optimization problem is a major challenge. It is also unclear which characteristics of a system are relevant for making good planning decisions, or which effects have an influence on the performance of the selected plan. Here, the integration of approaches from data analysis and optimization gains importance. Very promising for the future seems the way to start with generic base models to describe an application and to learn both the evaluation function and the specific constraints from the available data. This form of automatic model building will be much more appropriate for today's constantly changing planning conditions, where one often has to deal with a constant incoming of new data that must be immediately incorporated into the next control action for the system to keep it in the optimal state.
In particular, the ADA Lovelace Center develops techniques that are able to adapt to the dynamics of a given system and make optimal decisions for it. As a result, the decisions »learned« in this way will, over time, and with more training data, increasingly reflect real-world, time-varying conditions. The exploitation of this technique for the derivation of optimization models paves the way towards self-learning mathematical decision models, which represent a major advance in the field of automatic planning and control. Methods previously available for this problem, such as multilevel stochastic optimization, often fail here because of their exorbitant computational cost. Online learning offers an alternative because its philosophy involves considering each data point only once, which leads to significant decoupling along the temporal axis and thus to significantly lower computational complexity. It also ensures that no more recent knowledge can be forgotten, as more distant observations are given significantly less weight than recently recorded data.

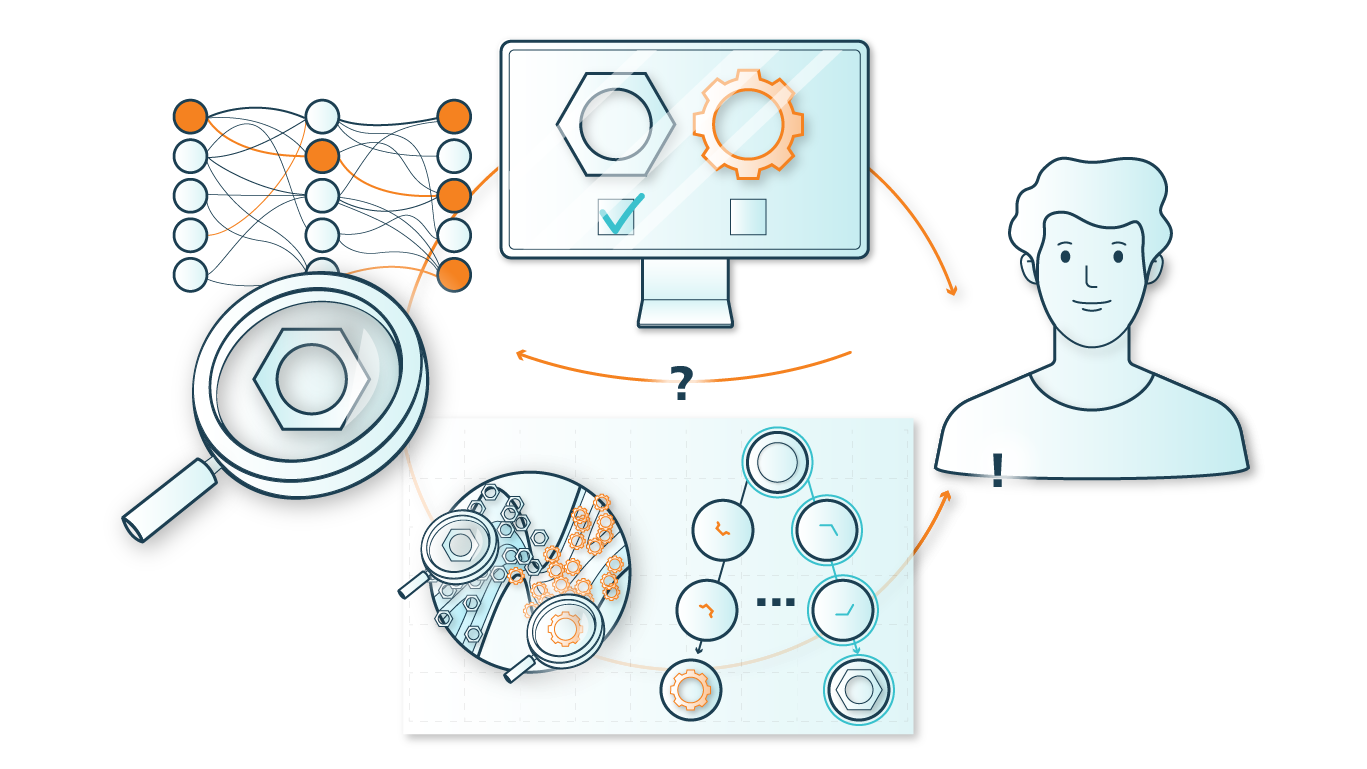
Learning optimization methods

Learning optimization methods are also an essential contribution to a better understanding of a given system. In many areas of practical planning in a company, the decisions made are based on implicit, non-formalized rules (sometimes »gut decisions«). These are not bad in themselves, but are often difficult to understand and thus difficult to automate. Also, this form of expert knowledge is often lost when the responsible employees change companies or retire. Learning optimization models enable a company to cast the planning knowledge that is implicitly available at the company into a mathematical form that allows this knowledge to be made understandable and usable for automated decision making. The ADA Lovelace Center is one of the pioneers in this field of research and provides significant impulses in a field that is capable of increasing the competitiveness of German industry quite decisively.

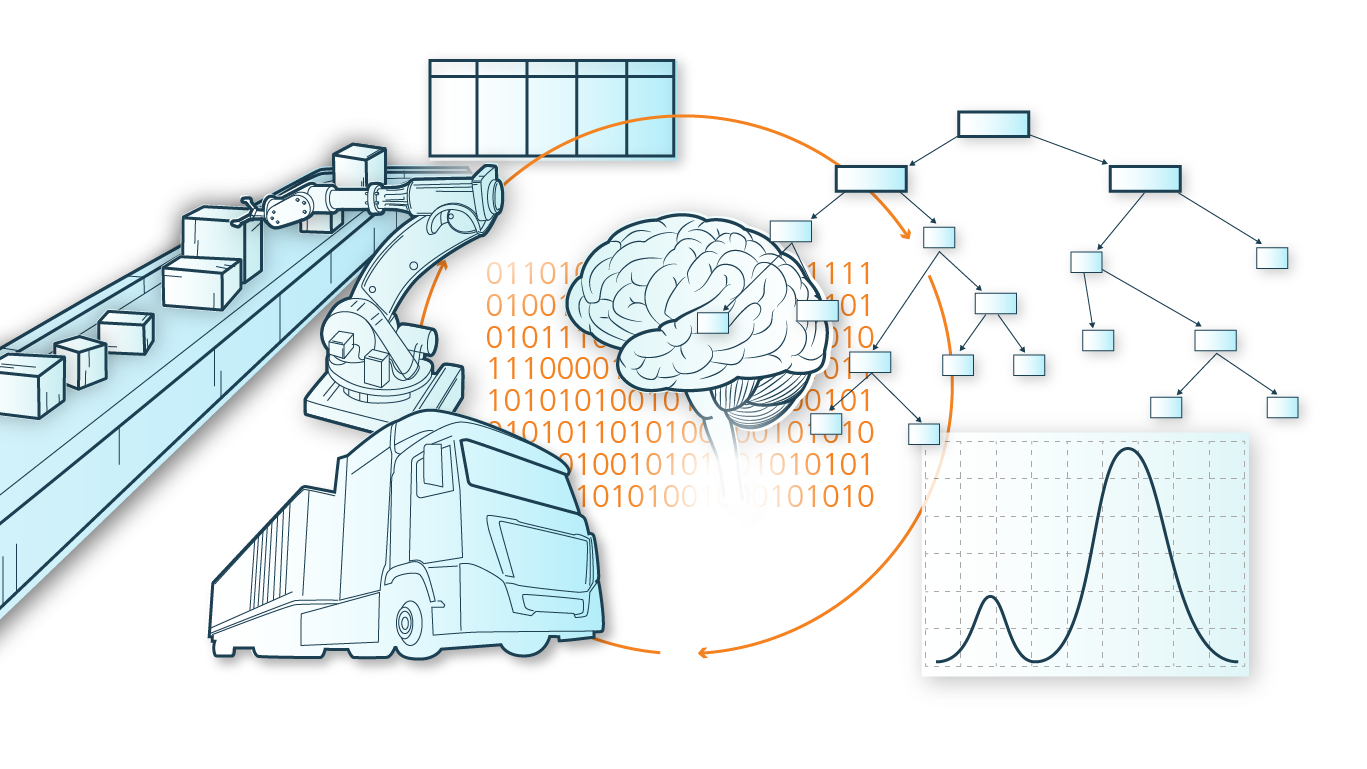
Another challenge of modern optimization methods is the reduction of model complexity. This is of immense importance especially in view of the ever increasing amounts of data that have to be included in decision making. Modern mathematical methods promise a remedy for the dilemma that exact integer optimization methods usually have a runtime that grows exponentially with the input size. Separating relevant from irrelevant parameters by integrating data analysis techniques and optimization algorithms allows signal and noise to be distinguished from each other even with very large data sets. This representative selection of effects in the objective and constraints of the chosen optimization model can thus significantly reduce computation time. An example of this is the recent development of learning algorithms for selecting representative scenarios in optimization under data uncertainty. The latter represents a technique for making decisions that remain high quality and actionable under uncertain input data (e.g., based on measurements or forecasts). Such algorithmic methods, which allow the selection of representative scenarios among a large variety of conceivable scenarios, are an important contribution to the applicability of these methods in practice. Here, too, the ADA Lovelace Center is setting internationally visible accents with its research.

Finding the right mix with mathematical optimization

Mathematical optimization methods are indispensable for the description and efficient planning of complex systems. Among other things, they occur where the sheer number of components interacting in them already causes an explosion in the combinatorics of admissible solutions. Especially in the context of logistic decision processes, the optimization of complex systems plays an essential role. One thinks here, for example, of production in the food industry. There, raw materials have to be mixed in certain, fixed ratios in order to produce the finished products. The requirements for the ingredients as well as the legal specifications have become so complex in the meantime that just setting up an admissible assignment of the raw material batches to the mixing orders is already a very difficult problem; not to mention finding the most cost-saving plans possible. In the application »self-optimizing adaptive logistic networks« we develop mathematical models and algorithms to solve such problems.

Timetable optimization for energy savings in rail traffic

Every day, around 30,000 trains are on the move in the German rail network, and these have to be taken into account when drawing up timetables. In recent years, in addition to the usual requirements for timetable design, such as punctuality and operational safety, the aspect of energy consumption has become increasingly important. Furthermore, if one also wants to optimize the energy consumption of trains, including their motion dynamics, as part of timetable optimization, an optimization problem with physical constraints associated with switching operations arises. The mixture of continuous and discrete part of the problem leads to the fact that one can resort to methods of the respective other discipline for the solution. Thus, differential equations often have to be linearized before discrete optimization techniques can be used again. This can be done, for example, on the basis of so-called piecewise linearizations. This technique allows to linearly approximate nonlinear functions in an optimization model by setting grid points. Such and other techniques are developed and applied in the ADA Lovelace Center in the application »Driver Assistance Systems in Rail Traffic«. In a joint project with the public transport company VAG, these techniques are being used to increase the energy efficiency of the Nuremberg subway system.

Optimal network utilization in direct current networks

Power electronic components form the core of countless applications and systems in industry, energy technology, building services and mobility. Built-in power converters continuously measure parameters such as current, voltage, and their changes over time, and use them to indirectly determine the status of the connected overall system (for example, the energy grid, a manufacturing plant, a storage system, or an electric motor). In the application »Intelligent Power Electronics«, we develop mathematical models to optimize the stability of DC networks with the help of these data. The goal here is to select suitable components and adjust the software control in order to optimally align the network to a certain range of load scenarios. Since the simulation of the load flow in DC networks is too complex to integrate it directly into an optimization model, we train classification models such as decision trees to represent the complex influences of components and software on network stability. These constraints are reformulated in mixed-integer form to approximate the learned relationships in a much simpler form in the optimization model. Specially adapted decomposition algorithms ensure faster computation of the solution. Thus, we obtain efficient methods for the computation of optimal network designs.